|
Home / sperimentazione / Che dimostrazione! / Terze 2016-17
|
|
Edizione 2016-17 per le classi terze |
|
|
Date degli incontri Lunedì 28 novembre 2016 Incontro n.1 dalle ore 15:00 alle ore 17:00 AULA CASTIGLIANO E' possibile scaricare le schede utilizzate nell'incontro del 28 novembre qui. Nelle prime due schede abbiamo voluto mettere a confronto le loro prestazioni di tipo argomentativo e dimostrativo su un problema, la cui soluzione poteva non essere evidente per chi è abituato a riconoscere l’equivalenza di figure piane attraverso la somma di aree di figure congruenti e non invece a riconoscere l’equiscomponibilità attraverso la differenza tra le aree di figure equicomposte. 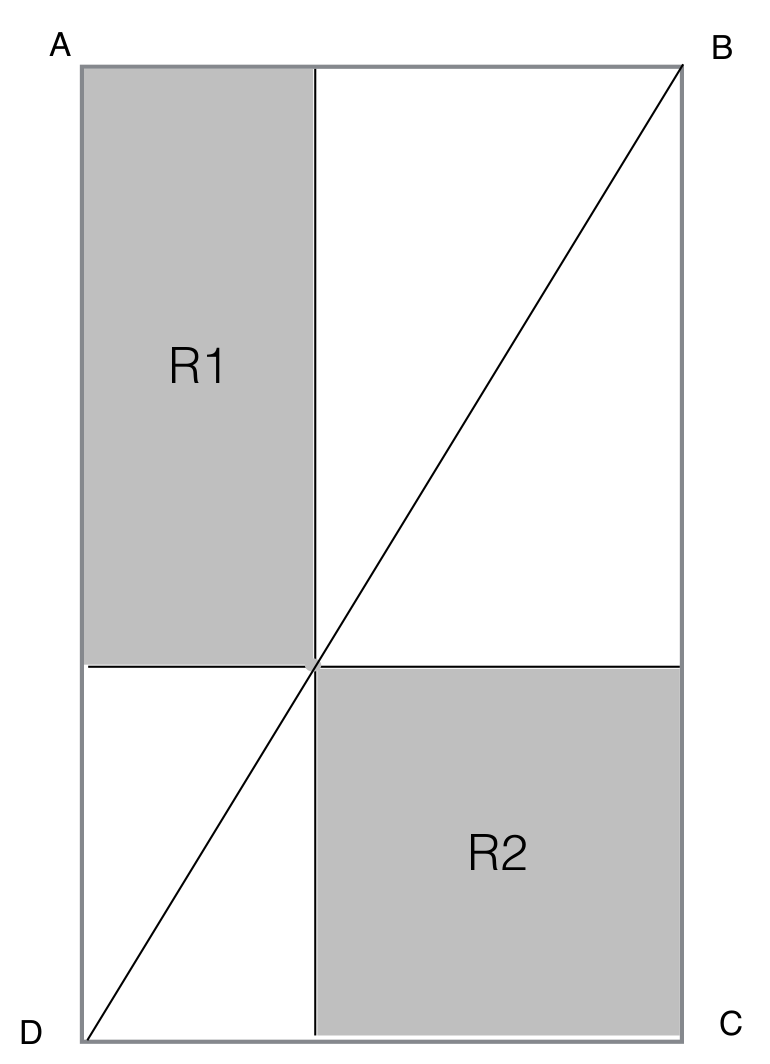
Il problema chiede di stabilire se l’area di R1 è equivalente all’area di R2, dove R1 e R2 sono due rettangoli ottenuti a partire da un punto qualsiasi sulla diagonale. I ragazzi hanno riconosciuto subito l’equivalenza delle due figure e hanno anche saputo giustificarla abbastanza correttamente. Per alcuni c’è stata solo una risposta corrispondente ad una vera a e propria dimostrazione, altri sono riusciti a dare prestazioni diverse fornendo prima una giustificazione verbale della propria affermazione sulla equivalenza, e poi strutturando la dimostrazione facendo riferimento a teoremi noti. Abbiamo anche trovato una soluzione molto originale che utilizzava il secondo teorema di Euclide. Un punto importante emerso dalla discussione è che tutti erano ben consapevoli che in una dimostrazione esistono assiomi e teoremi a cui fare riferimento per affermare degli enunciati. Minore esperienza, com’è d’altra parte naturale, abbiamo notato sul riconoscimento delle regole di inferenza. Questo è un aspetto che si potrà approfondire. La terza scheda era pensata come una prova di tipo marcatamente sintattico. E’ stata fornita la dimostrazione dell’enunciato:
Anche questa prova è andata abbastanza bene: per alcuni solo una inversione, su un punto poco significativo della dimostrazione. La quarta attività ha permesso di ragionare sulle successioni: a partire da un quadrato di lato 1 cm, disegna il secondo in modo che abbia un lato coincidente con una delle diagonali di questo quadrato, il terzo con un lato coincidente con la diagonale del secondo e così via. Quale è la lunghezza del lato dell’undicesimo quadrato? Quale sarebbe quella del lato del centesimo quadrato? Abbiamo osservato che, in generale, gli studenti hanno affrontato il problema in modo algebrico, facendo poco ricorso al disegno. Questo approccio astratto per alcuni ha costituito un problema di controllo sulla correttezza della risposta trovata, mentre per la maggioranza ha rivelato una tendenza all’astrazione e all’uso degli strumenti formali dell’algebra. La quinta attività, relativa ad un problema proposto ai vari gruppi, si è rivelata un’esperienza significativa per i ragazzi: è possibile costruire un triangolo equilatero (in cui la lunghezza del lato misurata in centimetri è un numero intero) che abbia perimetro coincidente con l’area? Quasi tutti sono riusciti a dimostrare algebricamente che la soluzione al problema non c’era, tutti hanno spontaneamente ragionato su casi generali, senza fermarsi a casi particolari e a verifiche su esempi.
Il gruppo dei ragazzi iscritti si è subito rivelato vivace e con una buona preparazione e buone capacità. Ciò ci incoraggia nell’obiettivo di proporre approfondimenti su varie tematiche relative ad argomentare e dimostrare. Lunedì 23 gennaio 2017 Incontro n.2 AULA CASTIGLIANO E' possibile scaricare le schede utilizzate nell'incontro del 23 gennaio qui. Le attività programmate erano diverse e non siamo riusciti ad attuarle tutte, abbiamo preferito lasciare il tempo che era necessario a i ragazzi. In realtà, entrando nel merito delle dimostrazioni, i ragazzi hanno mostrato difficoltà, probabilmente perché quest’anno tale attività, prevalente in geometria euclidea nel biennio, è stata soppiantata da nuove esperienze in altri ambiti teorici. Non mancano, anche per noi, a posteriori, riflessioni sulla formulazione delle schede, che potrebbero essere migliorate apportando alcune correzioni al testo. Appare però importante che il gruppo sia numericamente consistente, come quello costituito inizialmente. L’incontro del 23 gennaio si è svolto con un gruppo molto ridotto di studenti, e ciò non ha certo favorito la discussione e le attività di gruppo, fondamentali per le proposte da noi formulate. Ecco un commento più puntuale alle schede. La prima scheda propone la seguente situazione geometrica: TEOREMA ABCD è un parallelogrammo. I è il punto di intersezione delle diagonali, E il punto medio di CB e F quello di CD. Le rette AC ed EF si incontrano in M. Tesi: M è il punto medio di EF. Il teorema è centrato sulle applicazioni del Teorema di Talete e del suo “inverso”. Subito dopo si propone agli studenti di dimostrare il teorema, utilizzando gli enunciati riportati in un riquadro, corrispondenti appunto ai due teoremi di cui sopra e alla definizione e alle proprietà di un parallelogramma. Gli studenti non hanno riconosciuto con chiarezza il teorema di Talete, distinguendolo dall’inverso. Alcuni (pochi per la verità) li confondono tra loro. Nelle loro dimostrazioni a volte i teoremi citati nel riquadri sono elusi e si ricorre alle relazioni di congruenza e similitudine, anche con modalità più complicate nella suddivisione della figura. Nel complesso le dimostrazioni sono, almeno in parte, corrette. Alcune imprecisioni od omissioni sono presenti nei vari passaggi. La seconda scheda ripropone le attività della scheda precedente, ma su un altro teorema: TEOREMA Da un punto P esterno ad una circonferenza di centro O conduci una tangente che interseca la circonferenza in A. Da A conduci poi la perpendicolare a PO che interseca la circonferenza in B e in C (con B più vicino a P). Dimostra che AB appartiene alla bisettrice dell’angolo PAE. Gli studenti hanno avuto bisogno di un po’ di aiuto per produrre la dimostrazione. Il lavoro di esplicitazione completa del discorso dimostrativo è difficoltoso, e mostra l’opportunità di ulteriori attività in cui agli studenti sia esplicitamente richiesto di argomentare sulle loro affermazioni, o di citare puntualmente i teoremi che le garantiscono. Anche la costruzione di un nuovo schema “alla Duval” li ha portati ad affrontare un certa difficoltà. Naturalmente, ciò è normale in quanto queste esperienze di carattere metacognitivo passano attraverso una molteplicità di momenti esercitativi e di riflessione, che sarebbe bello se potessero proseguire a scuola, ogni volta che se ne presenti l’occasione. La terza scheda ripropone le attività della scheda precedente, ma su un altro teorema: TEOREMA Considera due circonferenze tangenti esternamente nel loro punto comune A e considera, oltre alla tangente in A, un’altra retta tangente a entrambe nei punti P e P’. Tesi: l’angolo PAP’ è retto.
Lunedì 30 gennaio 2017 Incontro n.3 Laboratorio didattico (IV piano Dipartimento di Matematica) E' possibile scaricare le schede utilizzate nell'incontro del 30 gennaio qui, utilizzate per un lavoro in ambiente di geometria dinamica svolto nel laboratorio con Geogebra. I problemi proposti erano concepiti proprio perché consentissero la metodologia appropriata all’interazione con il micro mondo di Geogebra. Dopo aver effettuato la costruzione, gli studenti possono esplorare la figura dinamicamente, cogliendo le proprietà varianti e invarianti. Da questa interazione con la figura si possono formulare congetture, che devono essere esplicitate dai ragazzi anche verbalmente. A quel punto si pone il problema di dimostrare la verità o la non verità della congettura. La dimostrazione diventa quindi un passo ulteriore, rispetto all’evidenza di quanto si osserva e alla verifica su particolari esempi. Non tutti gli studenti erano abituati ad usare Geogebra, tuttavia è bastata una breve introduzione perché i ragazzi riuscissero a lavorare tutti, con ottimi risultati. Il primo problema pone di fronte ad un quesito che inizialmente porterebbe a congetturare che l’angolo che si chiede di considerare, formato da due bisettrici di un triangolo, sia retto. In realtà la dimostrazione chiarisce un risultato inatteso: l’angolo in questione non può essere retto, a meno che il triangolo non sia degenere. Il teorema è centrato sulle applicazioni del Teorema di Talete e del suo “inverso”.
I ragazzi hanno lavorato molto bene, sono arrivati tutti alla conclusione corretta, dimostrando, a volte anche con soluzioni originali, che l’angolo considerato diventa retto solo se il triangolo diventa degenere. Il secondo problema, tratto da un lavoro della professoressa Mariotti (Università di Siena) ci è apparso subito come interessante poiché motiva all’esplorazione dinamica: si tratta di un problema in cui lo strumento Geogebra è indispensabile per verificare che la posizione del tesoro non dipende da quella dell’albero di melo scomparso. Anche in questo caso gli studenti hanno lavorato in maniera molto produttiva in gruppo. Dopo aver verificato che la costruzione del punto in cui si trova il tesoro non dipende dal punto M, pur avendolo utilizzato per trovare T, si sono posti il problema di come costruire il punto in cui si trova il tesoro senza utilizzare M. Nonostante il problema non sia banale, siamo molto soddisfatti del lavoro prodotto dai ragazzi.
Lunedì 13 febbraio 2017 Incontro n.4 AULA B.5.4 E' possibile scaricare le schede utilizzate nell'incontro del 13 febbraio qui. Obiettivo di quest’ultimo incontro era quello di mettere a confronto la dimostrazione in teorie diverse, ad esempio quello della geometria euclidea e quello della geometria analitica. Si è partiti da un problema (scheda 1a), posto come un’attività in cui si richiede di verificare alcune proprietà per una figura assegnata. Nella scheda successiva (1b) si ritorna sulle proprietà appena verificate, poiché è possibile generalizzarle se si ritorna ai teoremi noti nella geometria euclidea. Ciò voleva sollecitare la discussione sul fatto che spesso in geometria analitica è possibile riconoscere proprietà più generali, che nel piano euclideo si dimostrano indipendentemente dalla loro posizione. Nelle schede successive è stata proposta la dimostrazione euclidea e analitica dello stesso teorema: Le altezze di un triangolo si incontrano in un medesimo punto La dimostrazione euclidea era guidata, in quanto non sempre questo teorema si dimostra nel comune percorso del biennio, tuttavia i ragazzi l’hanno ricostruita con facilità, a partire dall’analisi della costruzione geometrica. La dimostrazione analitica è stata solo accennata. L’ultimo problema, che ritenevamo interessante da studiare riguardo agli atteggiamenti dei ragazzi, è stato solo analizzato sommariamente. Si trattava di risolvere uno stesso problema con metodi diversi, analiticamente, o trigonometricamente, oppure riconoscendo alcune proprietà viste in geometria euclidea. Si è constatato che una risoluzione trigonometrica i ragazzi non potevano ancora farla, e soprattutto i tempi richiesti per la discussione sarebbero stati maggiori di quelli disponibili. L’incontro è stato reso poco significativo, nonostante ne ritenessimo importante il senso nel complesso del progetto, per varie difficoltà:
Giovedì 30 marzo 2017 ore 14:30 - 16:00 Incontro con gli insegnanti per fare il bilancio del primo anno e per iniziare a programmare il secondo anno Sala lavagne (V piano Dipartimento di Matematica) |
|
| Responsabile dell'attività Chiara Andrà |






